When the words came tumbling out of my mouth,
I felt it all goin’ south,
But I kept on talkin’
‘Til you started walking.
Now I’m trying to dig my way out.
Ain’t I got a right to be wrong?[1]
I was a whiz kid in college.
You know, the kind of kid my professors wanted to whiz on. The reason: I was quick to argue, often too quick. College presented a very competitive environment to me. Rather than learn from others who actually knew better and had something to teach me, I often let myself get caught in the trap of thinking that competitive posturing would advance my career. I know now that never happens in the business environment among mature adults, but in the mind of a sophomore engineering student surrounded by thousands of people all competing for grades and corporate placement, winning seemed like a fine goal to have in mind. #winningOne afternoon during diffycues[2] recitation, our teaching assistant posed a problem. Consider two blocks, each with a mass M attached by a spring to a wall. Each block rests on a surface with known and identical coefficients of friction. The only difference between the blocks is that one is on the Moon’s surface and the other on Earth at sea level. What is the difference, if any, of the oscillation period of the mass-spring systems?” I knew the answer. “The block oscillates more slowly on the Earth!” The teaching assistant smiled and asked, “How do you know that?”[3] It was about to get even hotter on that July afternoon in Georgia.
Punctuating each phrase with my pointed finger, I began by “ explaining” that the weight of the block on the Earth would be greater; therefore, the downward force on the surface would be greater; therefore, the resistive friction force to the motion would be greater. A greater opposing force would create a greater negative acceleration (engineers like to say “negative acceleration” rather than “deceleration” because it makes our words sound more precise), reducing the period of oscillation.
My intuition was completely wrong.
But before I let the math prove to me that the TA was, indeed, correct to say that there is no difference in the oscillation period, I jumped up in my seat and declared, “I garandamntee you that the block on the Earth will oscillate slower!” Hopefully, I was just faint with the heat of July.
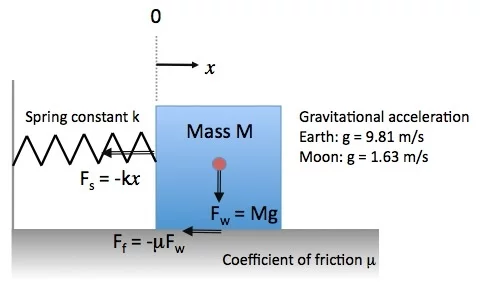
I would garandamntee you that this mass-spring system with an opposing friction force oscillates more slowly on the Earth than on the Moon, but I would be wrong. :/
There are usually several working assumptions that simply go unstated when people argue or take sides. The most common is that one person is right (namely, themselves) and the other party is wrong. That should not be surprising. I mean, how many times have you heard someone declare, “I don’t care what you say, I’m absolutely wrong about this, and I’ll defend my position to the grave!”
From this starting point, if this assumption is at work, it is not logically possible for both opposing parties to be correct. In this case, both parties become victims of the fallacy of bifurcation and then loyal adherents of the law of the excluded middle. Throw in a little ego and soon you see impasse, increasing irrational behaviors, and the potential for serious conflict. When you find yourself in this situation, it’s usually a good idea to consider if there are more than two possible discrete positions (i.e., not X vs Y, but X vs Y vs Z vs … ) or if the problem might better be framed of as a matter of degree (i.e., not X vs Y, but X on some position in an interval between poles). In my brief and limited career, I’ve found it rare that the complex issues that are worth exploring with serious attention present only two positions that must be mutually exclusive.
Another assumption that both parties usually begin with is that each (to the exclusion of the other) has all the information that can be known on the issue at hand. When you pause to think about this with quiet reservation, you realize that this assumption is just arrogant and stupid in the extreme. (I know because I have all the information about it.) Seriously, one would be hard pressed to claim that this assumption is based on ignorance alone: “What? You mean I can’t possibly have all the information about a matter?” When you find yourself in this situation, it’s usually a good idea to consider which of your assumptions could be disconfirmed if new information came to light. This isn’t easy. It requires thinking about which assumptions we take as “Inconceivable!” that could, in fact, be true.
[youtube http://www.youtube.com/watch?v=1-b7RmmMJeo?rel=0&w=420&h=315]
One last assumption I’ve found that many people actually find surprising to consider is this: it’s possible for both parties to be wrong, or worse, not even wrong[4]. Funny enough, if the first two assumptions discussed above are in play, then both parties are, in fact, very likely wrong. Yet, if both parties are wrong, this allows them to frame the problem in much more constructive terms, rather than as opposing points of view.
Most problems that are sufficiently interesting and worthy of our protracted attention are large enough that a single perspective isn’t broad enough to capture all the requisite information to resolve it, much less possess all the computing power required. Our best efforts at problem resolution occur when we frame the problems from multiple perspectives of goals and preferences, degrees of belief about important outcomes, and the decision options we could exercise to obtain our goals. When viewed this way, we see that there are likely multiple creative solutions, and the most valuable solution is probably one that neither party, with his limited view, could perceive alone. Yeah, we have a right to be wrong, but we don’t stand a chance to achieve much progress until we admit that we are wrong.
A few years ago I lamented to a mentor that my colleagues and I couldn’t agree to a solution about a problem attended by a significant amount of argument. He responded, “I’m not so concerned that people find a way to agree. I’d rather they find a way to constructively disagree. The agreement will come out of that.” In fact, it did, but we didn’t get there until we recognized that we were wrong.
- McCLINTON, DELBERT. Right to Be Wrong, Cost of Living. New West, 2005. Compact Disk.
- Differential equations, for the uninitiated.
- One of the best lessons I gained from my time at Georgia Tech was learning to ask the question: “How do you know that?” I now consider asking this question a type of moral obligation.
- By “not even wrong,” I mean that both parties have failed to frame their problem in a way that is predictable or falsifiable, that is, in such a way that is resolvable by human consideration.






